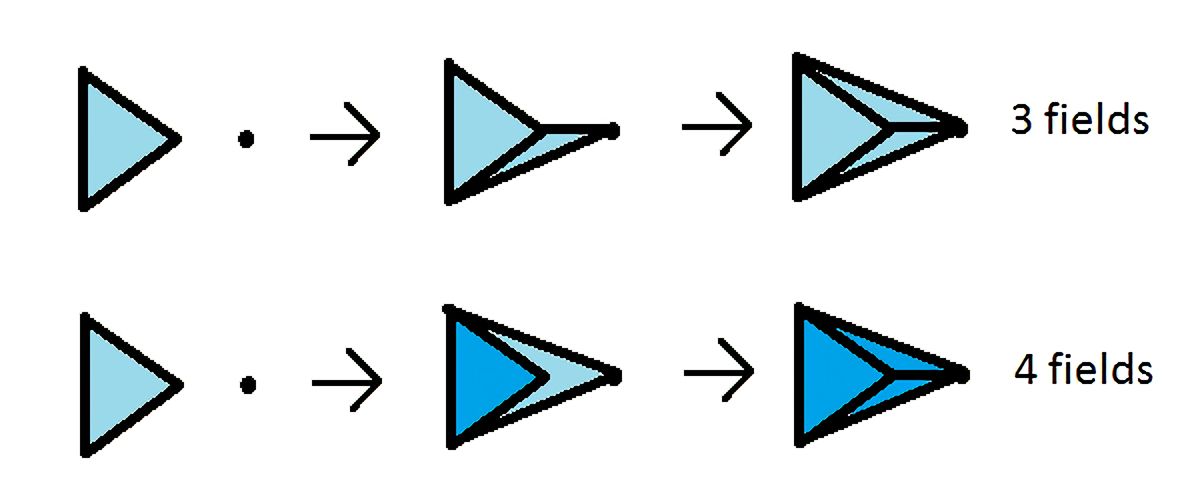
如何快速有效的构建多重,是想要获得大量ap所需要考虑的。当然熟练如我已经可以随心所欲做多重了,跟那些xjbl玩家可不一样。
原文来自G+,据说是某复旦大佬写的
可在此参考最终结论和操作步骤: http://m.guokr.com/post/569758/
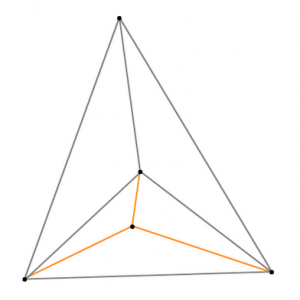
被凸n边形link包围的m个portal,最多且必然可连出(3m+n-2)个field
这句听起来有点拗口的话,实际上回答了一个问题:当地图上有乱七八糟一堆portal时
最多能从中连出多少个field?计算方法是:
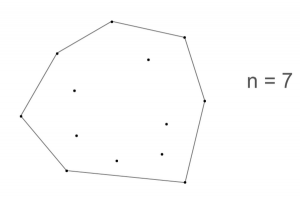
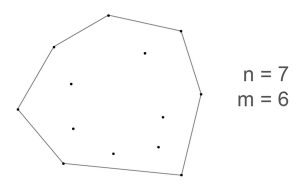
1. 先将最外面一圈的点连起来,数一下有多少个顶点(n)
2. 数一下内部围住了多少个点(m)
3. 代入公式计算:可连出(3*6+7-2)=23个field
以下是证明过程:
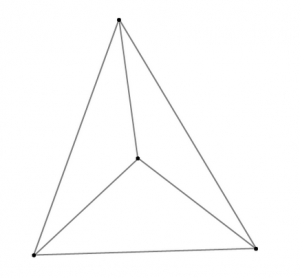
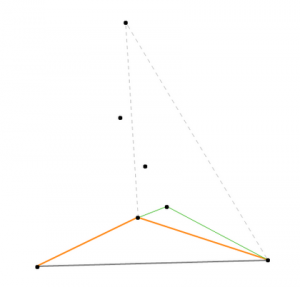
一个三角形内部有一个点时可以做4个field,这个相信大家已经很熟悉了吧
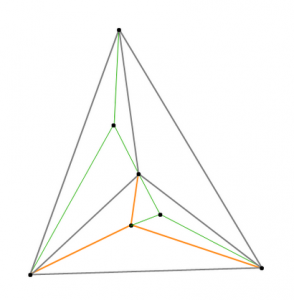
当三角形内有2个点时,可以任意选取一个点将大三角形分成3个小三角形,则剩下的一个点必然落在某个小三角形内,从而可以再用以上的方法分成3个三角形。
那么当三角形内有若干点的时候,可以反复用以上的方法划分,也就是说三角形内每有一个点,可以多做出3个field。
用这种方法可以保证连出最多的field,因为他实际是一个Appolonian Network (wiki),其特性之一就是拥有最多的内部三角形数。并且点的分布方式和选择顺序不会影响最终形成的三角形总数——这也很容易理解,因为点不管落在哪个三角形内,效果都是将其一分为三
但是ingress中要建立重复区域实际是有一些限制的,比如不能从field中间往外建link,并且建立link的先后顺序有一定要求,是不是对于任意分布的点一定能建成理论上限的field数呢?答案是肯定的,下面给出一种必然可行的策略:
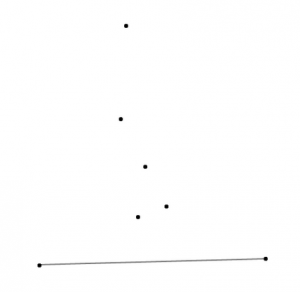
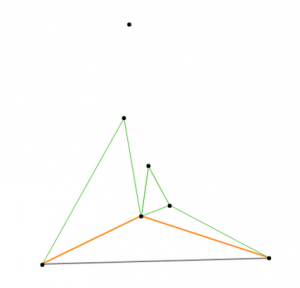
1. 随便连一条大三角形的底边
2. 在三角形内部选一个点与底边连成三角形,使构成的三角形内没有其他点(一定做得到)
3. 以新连成的边为底边,在他们各自的小三角形内重复做以上事情
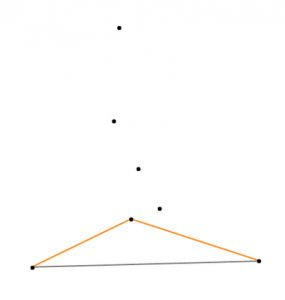
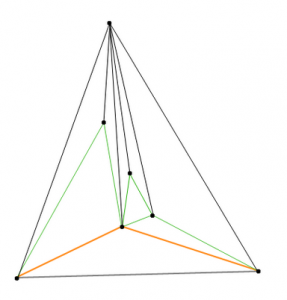
4. 全部做好以后应该是这样的
5. 然后从顶点到每个小三角形的顶点来一发(注意顺序)
实际情况下多数其实没这么复杂,只要稍微注意一下做link的顺序就行了。
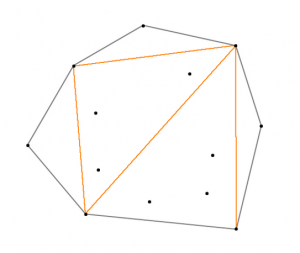
以上讨论了三角形内部的情况,对于n边形来说,总是可以通过连接顶点将其分割为n-2个三角形
对于任意分布的点来说,这个多边形是唯一的,并且一定是凸多边形;分割的方法同样不影响最终形成的field数,因为多边形内部的任意点必然最终落在某一个三角形中。所以内部的点(m)能够做出的field数为3m,加上分割多边形形成的n-2个field,最终能够做出的field数为3m+n-2。
几个推论:
- 多边形内部的点每个价值为3个field,边上的点每个价值 为1个field
- n=3时就是三角形,是这个结论的一个特例,能够在portal数相同的情况下做出最多的field
- 完美连接的情况下,用掉的key数量为 多边形的边数+分割多边形的link数+内部点数*3=n+(n-3)+3m=3m+2n-3
- 当边数很少,内部点数很多的时候,field数与link数之比趋近于1,也就是每一把key几乎都能做出一个field
那么就请大家多多利用以上的结论,利用有限的portal刷出更多的ap吧
END
本文被阅读了:2,321次